LeetCode 笔记 5:Search in Rotated Sorted Array
详解旋转排序数组的特性及如何在其中应用二分查找算法,包含多个 LeetCode 题目的解题思路
今天要讲的题目都使用到了二分查找(或者和二分查找紧密相关),同时又都是基于一个 Rotated Sorted Array。那么先从 Rotated Sorted Array 的特点讲起吧。
Rotated Sorted Array 的定义是这样子的:
There is an integer array
numssorted in ascending order (with distinct values).numsis possibly rotated at an unknown pivot indexk(1 <= k < nums.length) such that the resulting array is[nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]](0-indexed).
就拿 int[] nums = new int[]{0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; 举例好了,如果 nums 在 nums[4] 位置进行旋转,那么它将变成: {4, 5, 6, 7, 8, 9, 10, 0, 1, 2, 3} ,那么我们能够观察到几个特性:
nums被分成了两个区间,两个区间都是排好序的(严格上升)nums第二个区间的所有元素小于第一个区间的最小元素
拿 {4, 5, 6, 7, 8, 9, 10, 0, 1, 2, 3} 举例来说,从 nums[0] 到 nums[5] 是第一个区间( {4, 5, 6, 7, 8, 9, 10} ),这个区间是排好序的,从 nums[6] 到 nums[9] 是第二个区间,第二个区间也是排好序的。同时第二个区间的所有值均小于第一个区间的所有值。
根据这两个特性,我们就能够在子区间中使用二分查找来缩小查找范围了。如何在 rotated sorted array 中使用二分查找算法,请看题:
Search in Rotated Sorted Array #
题目 1 #
33. Search in Rotated Sorted Array:
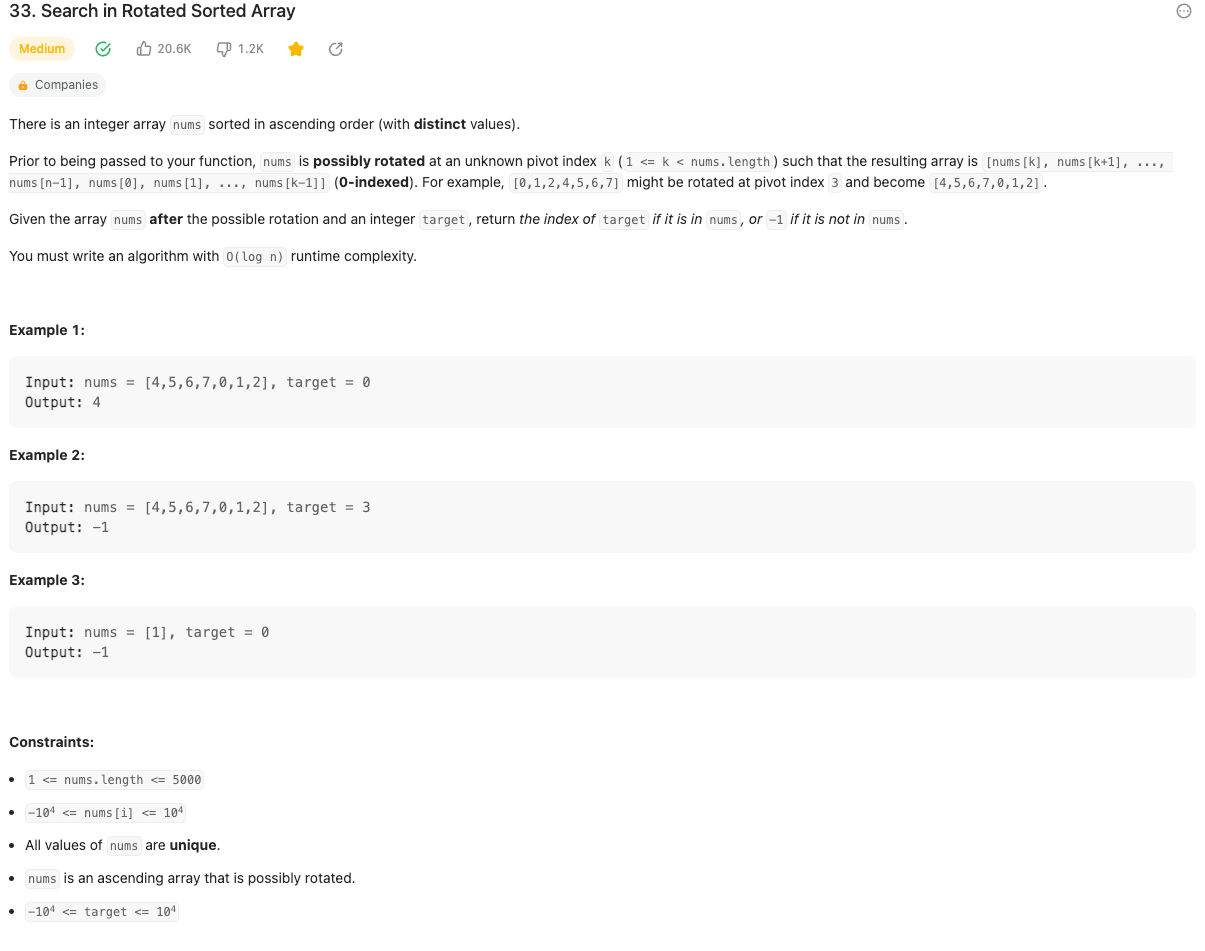
算法思路是这样子的:
- 定义
left, right, mid,计算mid,如果nums[mid] == target,那么就返回结果。 - 否则,我们需要缩小我们的查找空间。如何做呢?我们需要比较
nums[left],nums[mid]和nums[right]的大小来判断当前的子区间是否是排好序的(即判断[left, mid]及[mid, right]这两个区间是否是排好序的):- 如果
nums[left] <= nums[mid],那么说明[left, mid]这个子区间是有序的; - 如果
nums[mid] <= nums[right],那么说明[mid, right]这个子区间是有序的;
- 如果
- 在子区间是有序的前提下,我们再来判断
target是否在该子区间中,以及它和nums[mid]的大小关系。之所以要在有序的子区间内进行比较的原因是,二分查找算法只能使用在排好序的数据集合当中。 根据nums[mid]和target的大小关系比较,来移动左端点和右端点,就像寻常的二分查找那样:- 如果
nums[left] <= nums[mid],那么可能存在两种情况:nums[left] <= target && target < nums[mid],说明target在[left, mid]这个区间内,我们只需要将right左移到mid - 1处即可;- 否则,说明
target不在[left, mid]区间内,我们右移left节点即可。
- 如果是右半边子区间是有序的 (即
nums[mid] <= nums[right]),同样可能存在两种情况:nums[mid] < target && target <= nums[right]:说明target在[mid, right]这个区间内,右移left左端点;- 否则,说明
target不在这个区间内,我们左移right。
- 如果
- 重复以上步骤直到找到了
target,或left > right。
代码如下:
class Solution {
public int search(int[] nums, int target) {
int left = 0, right = nums.length - 1, mid;
while (left <= right) {
mid = left + (right - left) / 2;
if (nums[mid] == target) {
return mid;
}
if (nums[left] <= nums[mid]) {
if (nums[left] <= target && target < nums[mid]) {
right = mid - 1;
} else {
left = mid + 1;
}
} else {
if (nums[mid] < target && target <= nums[right]) {
left = mid + 1;
} else {
right = mid - 1;
}
}
}
return -1;
}
}
复杂度分析:
- 时间复杂度:
O(logN) - 空间复杂度:
O(1)
笔者认为,这类题目的关键点在于如何在找出可以使用二分查找的子区间上。因为 Rotated Sorted Array 的特性,导致我们无法确定 [left, right] 这个区间是排好序的,因此我们只能去分析更小范围的子区间的情况,也就是 [left, mid] 和 [mid, right] 这两个更小的子区间。一旦我们找到了排好序的区间,那么就可以使用二分查找算法的思想,来缩小搜索范围。
题目 2 #
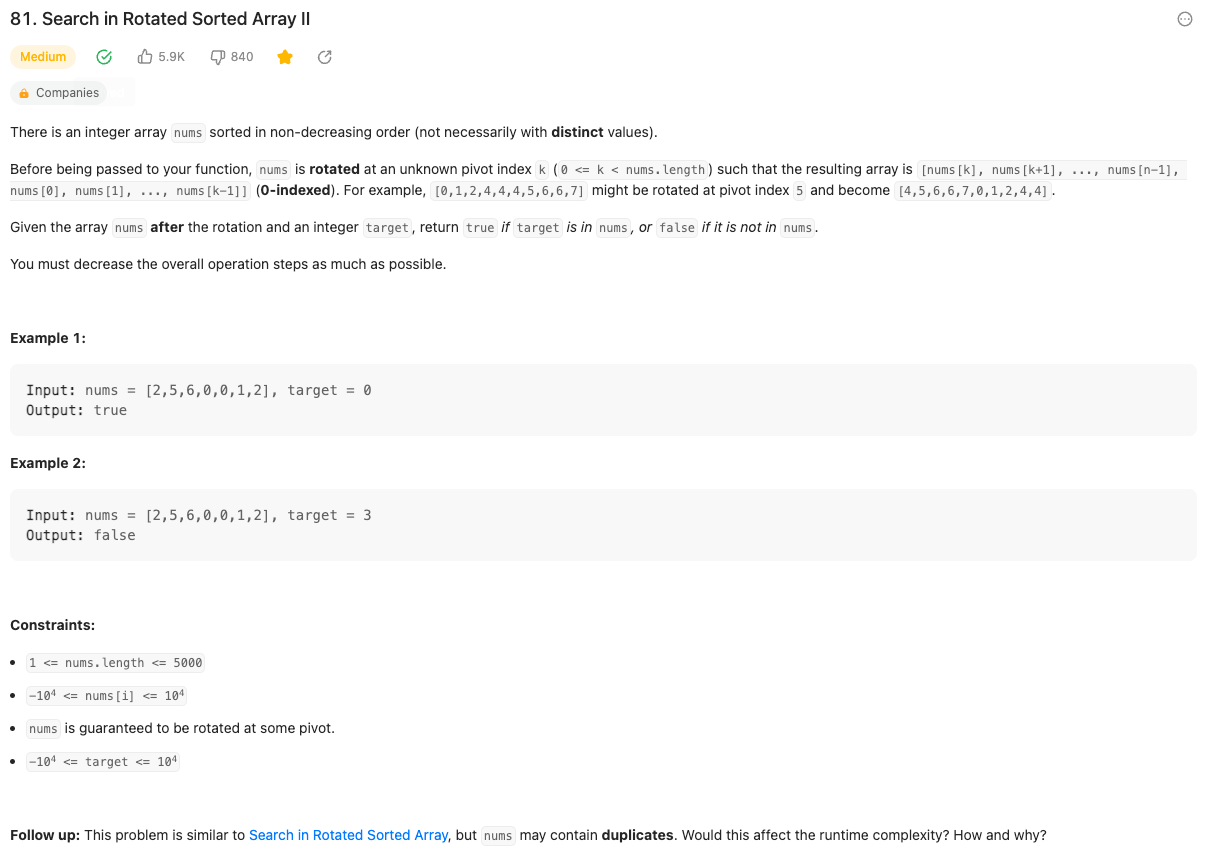
这道题目在上一道题目的基础上只有一个不同,那就是 nums 可能存在重复元素,而这将影响我们的算法,举个例子:
int[] nums = new int[]{1, 1, 1, 1, 1, 0, 1, 1, 1, 1}
假设 nums 是这个样子的,我们只需要演算一下我们算法的第一次迭代即可看出问题:
left = 0,right = 9,mid = 0 + (9 - 0) / 2 = 4;nums[left] <= nums[mid],同时,nums[mid] <= nums[right];
我们发现 nums[mid] <= nums[right] ,那么按照我们之前的想法, [mid, right] 这个子区间应该是排好序的,但是 {1, 0, 1, 1, 1, 1} 却不是一个有序的数组。问题就出在重复元素上。
解决方法其实也很简单,我们只需要略过这些重复的、影响对我们数组是否有序判断的元素即可,整体算法不变:
class Solution {
public boolean search(int[] nums, int target) {
int left = 0, right = nums.length - 1, mid;
while (left <= right) {
while (left + 1 <= right && nums[left + 1] == nums[left]) {
++left;
}
while (right - 1 >= left && nums[right - 1] == nums[right]) {
--right;
}
mid = left + (right - left) / 2;
if (nums[mid] == target) {
return true;
}
if (nums[left] <= nums[mid]) {
if (nums[left] <= target && target < nums[mid]) {
right = mid - 1;
} else {
left = mid + 1;
}
} else {
if (nums[mid] < target && target <= nums[right]) {
left = mid + 1;
} else {
right = mid - 1;
}
}
}
return false;
}
}
这两道题都是笔者之前博客 LeetCode 笔记 4:Binary Search 的5种变体应用 | caffcen’s blog 中提到的二分查找的第一种应用 Contains(即用二分查找判断排序数组是否包含目标)。
Search the Minimum in Rotated Sorted Array #
题目 1 #
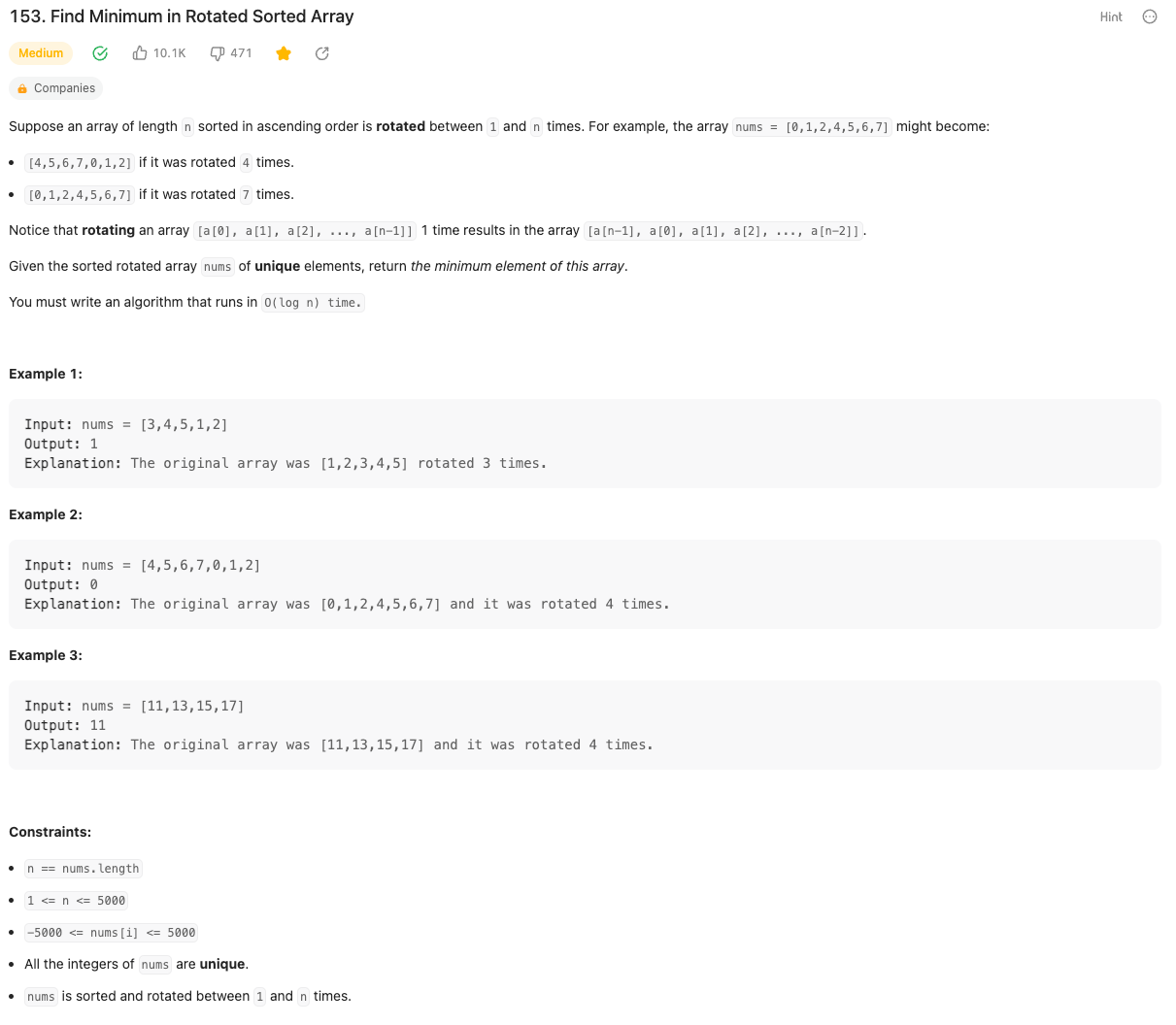
这道题目和之前题目的区别在于,之前题目给出了 target ,而这两个题目的 target 是 nums 中最小的元素。解决方法也很简单,只需要用到我们开篇提到的 rotated sorted array 的一个特性即可:
Rotated sorted array 的第一个子区间的最小值,大于第二个子区间的所有值。
既然第一个子区间的最小值都大于第二个子区间的所有值,那么整个 nums 中的最小值就是第二个子区间的第一个值了。那么目标就是去寻找第二个子区间的第一个值。
那么如何去寻找这个值呢?其实很简单,我们只需要做一定的转换即可:根据 rotated sorted array 的特性我们知道,第一个子区间的所有值均大于第二个子区间的所有值,那么我们二分查找时定义的右端点,一定小于左端点,即 nums[left] < nums[right] ,同时,第一个子区间中的所有值均大于 nums[right] ,它们也都不是我们要找的解。而题目的解即第一个值小于 nums[right] 的元素。
为了更好理解,我们定义这样一个有序集合 S = [a1, a2, a3, ..., an] ,同时 S 中的元素 a 表示 nums 的下标,且 a1 < a2 < a3 < ... < an 。同时,它们都满足 nums[a] < nums[right] 这一要求,也就是说 S 是一个合法的解集。那么,『求 nums 最小元素』这个问题,就可以转换成『求 S 这一解集中的第一个元素』这样一个问题。
经过这么一转换,可以看出这道题目和 LeetCode 笔记 4:Binary Search 的5种变体应用 | caffcen’s blog 中的 Index of least element greater than (or equal) to key,最小的大于(或大于等于)目标的下标算法有异曲同工之妙:它们都是使用二分查找去求解集的第一个元素。
class Solution {
public int findMin(int[] nums) {
int left = 0, right = nums.length - 1;
while (left < right) {
int mid = left + (right - left) / 2;
if (nums[mid] > nums[right]) {
left = mid + 1;
} else {
right = mid;
}
}
return nums[left];
}
}
题目 2 #
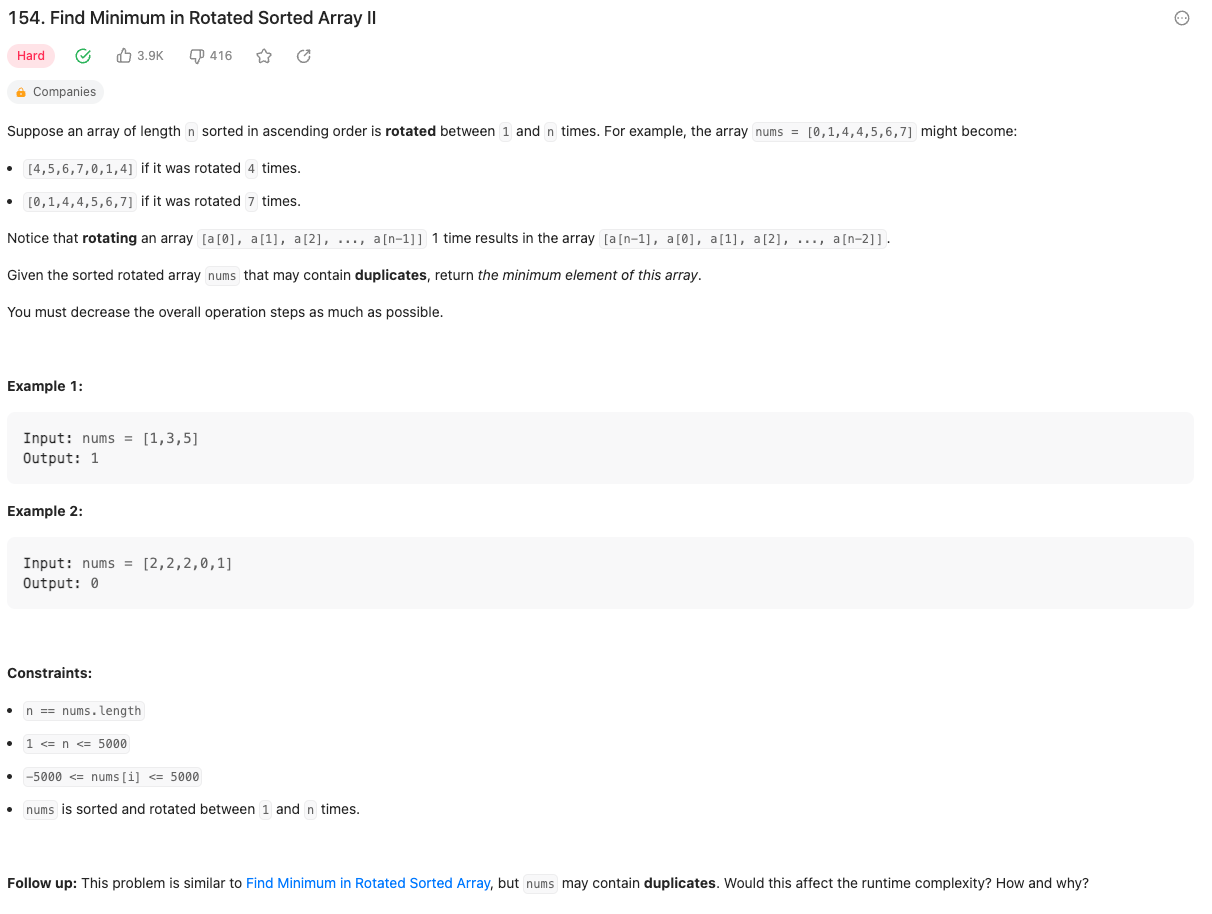
算法和上一题几乎一样,只是多了过滤重复元素的步骤,因此不再做过多赘述:
class Solution {
public int findMin(int[] nums) {
int left = 0, right = nums.length - 1;
while (left < right) {
while (left + 1 < right && nums[left + 1] == nums[left]) {
++left;
}
while (right - 1 > left && nums[right - 1] == nums[right]) {
--right;
}
int mid = left + (right - left) / 2;
if (nums[mid] > nums[right]) {
left = mid + 1;
} else {
right = mid;
}
}
return nums[left];
}
}
虽然不好理解,但实际上这两道题目都是用 Binary Search 去求解集中的第一个解,也就是 LeetCode 笔记 4:Binary Search 的5种变体应用 | caffcen’s blog 中的 Index of least element greater than (or equal) to key,最小的大于(或大于等于)目标的下标 这一算法。