Lihang Liu's Homepage

/Home

/Blog

/Archive

Lihang Liu's Homepage > Archive > 深入理解 B-Tree

深入理解 B-Tree

B 树是一种平衡多路搜索树，可以看做是对二叉搜索树（Binary Search Tree）的拓展。因为 B 树的自平衡以及允许一个节点存储多个值的特性，被广泛运用在数据库以及文件系统中，非常适用于存储大量数据。

要理解 B 树，最好的方式就是学习 2-3 搜索树——B 树的一种特例。

1. 2-3 搜索树 (2-3 Search Tree)

1.1 定义

2-3 搜索树是对二叉搜索树一种自然的扩充，二叉搜索树的任意一个节点只能存储一个 key、两个 links，但是 2-3 搜索树扩展了这一设定，2-3 搜索树允许存在以下两类节点：

  • 2-node：拥有一个 key 两个 links，2-node 和二叉搜索树中的节点完全等价，两个 links 分别指向左子树和右子树：
    • 左子树中的所有节点的 key 均『小于』当前 2-node 的 key；
    • 右子树中的所有节点均『大于』当前 2-node 的 key。
  • 3-node：拥有两个 keys 三个 links，3 个 links 分别指向左子树、右子树和中间子树：
    • 左子树中的所有节点的 key 均『小于』当前 3-node 较小的 key；
    • 右子树中的所有节点均『大于』当前 3-node 较大的 key；
    • 中间子树中的所有节点均大于 3-node 较小的 key，且小于 3-node 较大的 key。

这里大于、小于打引号是因为类型的大小关系往往是可以自定义的。

本文使用 key 表示存储数据的键，links 表示指向其他节点的引用，value 表示存储数据实际存储的值，在数据库以及文件系统中，value 可能是指向实际数据的指针。

2-3 搜索树支持搜索、插入、删除操作，这些操作的最坏、平均时间复杂度均为 O(longN) ， N 为 2-3 搜索树的数据总量。同时，2-3 搜索树总是高度平衡的，所有叶子结点到根节点的距离总是一致的。

本文将会对搜索以及插入操作进行详细分析。

1.2 搜索

在 2-3 搜索树中搜索某一个 key 是否存在，和在二叉搜索树中几乎一致：

  1. 判断 target 是否等于当前节点中任意 key，如果相等则返回当前节点；
  2. 如果当前节点是 2-node，那么将出现两种情况：
    1. 如果 target 小于 2-node 的 key，则递归地向左子树进行搜索；
    2. 如果 target 大于 2-node 的 key，则递归地向右子树进行搜索；
  3. 如果当前节点是 3-node，那么将出现三种情况：
    1. 如果 target 小于 3-node 中最小的 key，则递归地向左子树进行搜索；
    2. 如果 target 大于 3-node 中最大的 key，则递归地对右子树进行搜索；
    3. 否则，递归搜索中间子树；
  4. 如果当前节点是 null 说明，target 并未在 2-3 搜索树中，返回 null

1.3 插入

向 2-3 搜索树中插入一对 key-value 是一个相较于二叉搜索树的插入算法更为复杂的操作。2-3 搜索树能够保证任何情况下（无论输入数据插入的顺序是怎样的）都是高度平衡的特性和 2-3 搜索树的插入算法是紧密相关的。

插入算法总是从 root 节点开始搜索，搜索到叶子结点为止（搜索算法 1.2 小节已经讨论过了），再根据叶子结点以及插入 key-value 键值对和叶子结点中的 key 的比较情况来进行操作的。之后的讨论都是基于『已经搜索到需要往哪个叶子节点进行插入』进行讨论。

1.3.1 插入到 2-node 中

如果待插入的节点是一个 2-node，只需要将其变为一个 3-node 即可：

当往一个 2-node 中插入一个节点后，所有叶子结点都还位于它原本的位置上，没有任何节点的位置发生变化，也没有新增任何的节点，所以整棵树在插入操作后依然是高度平衡的，所有叶子结点到根节点的距离都没有发生改变。

1.3.2 插入到单独的 3-node 中

如果整棵树只有 root 这一个节点，同时 root 是一个 3-node，那么我们和面对 2-node 时是一样的，我们将待插入的 key 插入其中，让其暂时将其变为一个 4-node（拥有 3 个 keys 和 4 个 links）。然后，我们将这一个 4-node 分裂为 3 个 2-node：

  1. 我们将 3 个 key 中大小位于中间位置的 key-value 对向上分裂，成为当前 2-3 搜索树的 new_root ；
  2. 将 3 个 key 中最小的变为 new_root 的左子树；
  3. 将 3 个 key 中最大的变为 new_root 的右子树

当往一个是 3-node 的 root 中插入一组数据后，整棵树的高度增加了 1（这也是 2-3 搜索树高度增加的唯一情况，2-3 搜索树的高度增加依赖于新插入的数据使得 root 进行分裂），原来的叶子节点到新 root 的距离都增加了 1，所有叶子结点到 root 的距离还是相等的，因此 2-3 搜索树在这种情况下依然是高度平衡的。

1.3.3 往一个父节点是 2-node 的 3-node 插入数据

当往一个 3-node 节点插入数据后，和上一小节一样，我们需要将其短暂变为一个 4-node，之后变成 3 个 2-node，并将顺序大小排中间的节点向上分裂。

因为该叶子节点的父节点是个 2-node，我们只需要将其变为一个 3-node 即可，剩下的未向上分裂的『最小』、『最大』节点变成分裂上去的 key 的左右孩子节点即可：

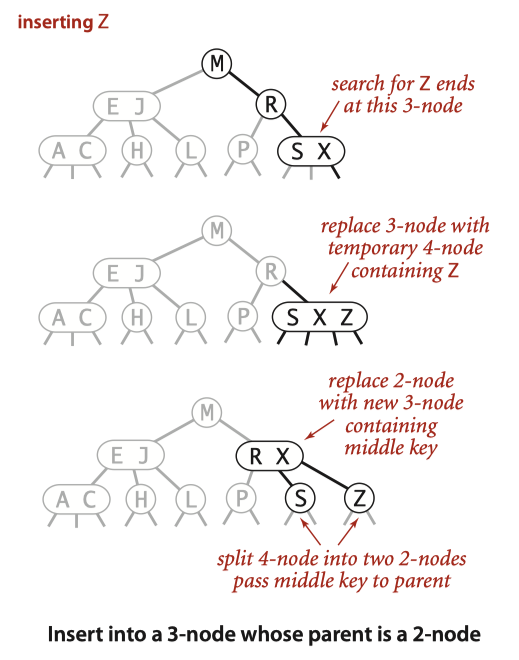
在这种情况下，从结果来看仅仅是一个中间节点从 2-node 变成了 3-node，没有新增任何节点，树的高度保持一致，因此在这种情况下 2-3 搜索树依然是高度平衡的。

1.3.4 往一个父节点是 3-node 的 3-node 插入数据

当向一个 3-node 叶子节点插入数据后，我们将其变为一个 4-node 后分裂成 3 个 2-node，并把大小排在中间的 2-node 向上分裂。

和 1.3.3 节不同的是，当前叶子节点的父节点是一个 3-node。那么，我们只能把向上分裂的 key-value 对加入其中，将其也变成一个暂时的 4-node，并分出 3 个 2-node，再将大小排中间的 key-value 对继续向上抛。

相信你此时一定能看出插入算法是如何递归地执行的了。我们将分裂得到的大小位于中间的 2-node 向上抛给父节点，如果父节点也需要进行分裂，那么递归地分裂、向上抛，直到某个父节点是一个 2-node，或者递归到 root 节点时 root 是一个 3-node，递归的步骤才会终止：

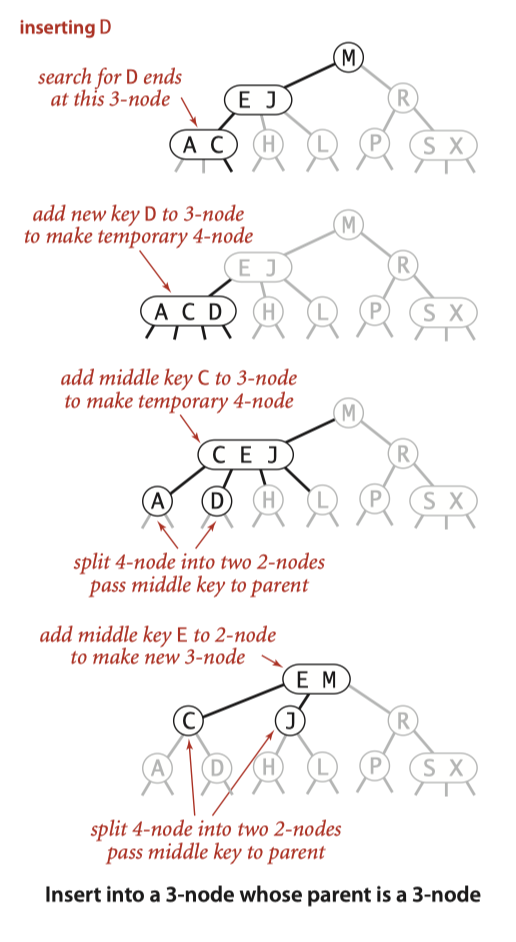
我们再来看看在这种情况下 2-3 搜索树是如何保持高度平衡的，只需要考虑两种情况：

  1. root 是一个 2-node，即便从叶子结点一路向上分裂，分裂到 root ，因为 root 是一个 2-node，那么情况将和 1.3.1 是一模一样的，我们只需要将 root 变为一个 3-node 即可。整棵树的高度没有发生任何变化，即便中间的路径可能发生了改变，但所有叶子结点在插入后还是在叶子结点的位置上，它们到根节点的距离依然是相同的。
  2. root 是一个 3-node，那么如果递归到最后需要向 root 进行插入，情况就和 1.3.2 一样，整棵树的高度增加 1，所有叶子结点到根节点的距离都加 1，那么 2-3 搜索树依然是高度平衡的。

也就是说，在这种情况下，2-3 搜索树的高度依然是平衡的。

1.4 2-3 搜索树插入算法总结

我们可以总结出 2-3 搜索树插入算法拥有这样的局部特性以及全局特性：

  1. 只有从叶子结点开始，沿着父子关系的路径往上，一直到根节点结束的这一条局部路径范围上的节点会受到影响，插入算法的影响范围总是局部的。
  2. 局部范围内的影响并不会破坏 2-3 搜索树的全局特性：2-3 搜索树在任意时刻总是高度平衡的，所有叶子结点到根节点的距离都相等。
  3. 2-3 搜索树只有当往一个类型是 3-node 的 root 节点插入时，才会导致导致整棵树的高度增加。
  4. 二叉搜索树的高度是往下增加的，而 2-3 搜索树的高度是往上增加的。

我们知道，二叉搜索树的高度和空间结构严重依赖于输入数据的插入顺序，在最坏情况下（比如顺序插入一组已经排好序的数据）的搜索、插入、删除时间复杂度将变成 O(N) ，而 2-3 搜索树因为它的分裂以及局部变更等特点，使得在任意情况下，插入、搜索、删除的最坏时间复杂度均为 O(logN) 。

2. B-Tree

B 树是对 2-3 搜索树的泛化，反过来说就是，2-3 搜索树是一种 3 阶 B 树。

2.1 B-Tree 定义

一个 m 阶 B 树可以看做是 2-3 搜索树的一种泛化，它拥有如下特点：

  1. 每个节点最多有 m 个子节点（ m 个 links）。
  2. 每个节点最多有 m - 1 个键值对（ m - 1 个 key-value pairs）。
  3. 每个内部节点至少有 ⌈m/2⌉ 个子节点。
  4. 根节点必须至少有 2 个键值对（两个 key-value pairs）。
  5. 所有叶节点在同一级别上出现。
  6. 一个具有 k 个子节点的非叶节点包含 k-1 个键值对。
  7. 关键字（keys）集合分布在整颗树中。
  8. 任何一个关键字（key）出现且只出现在一个结点中。
  9. 搜索有可能在非叶子结点结束 (树中所有结点都存储数据，与 B+树这一点不同)。
  10. 其搜索性能等价于在关键字全集内做一次二分查找（最坏时间复杂度 O(logN ）。

B 树的搜索、插入和删除算法本质上和 2-3 搜索树的搜索、插入、删除算法是一样的，它们的最坏时间复杂度都是 O(logN) 。学懂了 2-3 搜索树，你也就懂了 B 树的各种操作是如何执行的了。

Reference

  1. 2–3 tree - Wikipedia
  2. B-tree - Wikipedia
  3. 《MySQL 技术内幕——InnoDB 存储引擎》
  4. 《Algorithms, 4th Edition》by Robert Sedgewick, Kevin Wayne