LeetCode: Trie Data Structure & Related Problems

Introducing the trie data structure and how it can speed up prefix search

November 16, 2025 · 11 min read

In this post, I will talk about the Trie (Prefix Tree) data structure, how it is typically implemented, and several LeetCode problems that require it.

The Trie Data Structure #

Quote from Trie - Wikipedia:

[!quote]
In computer science, a trie (/ˈtraɪ/, /ˈtriː/), also known as a digital tree or prefix tree, is a specialized search tree data structure used to store and retrieve strings from a dictionary or set. Unlike a binary search tree, nodes in a trie do not store their associated key. Instead, each node’s position within the trie determines its associated key, with the connections between nodes defined by individual characters rather than the entire key.

The Trie data structure is a tree-like data structure where each node stores pointers to children. Each node in a Trie represents a char, and a string the Trie stores can be concatenated with all chars along the path from the root node to the end node (note that an end node could be an internal node, it is not necessarily a leaf node).

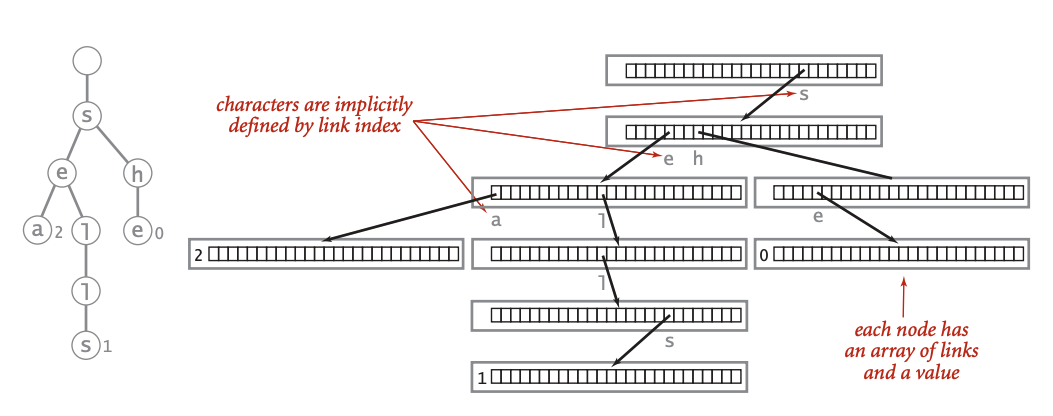
Trie is especially useful when querying whether a string or a prefix is present or not in O(L) time, where L is the length of the string. It has two main API: insert and search.

insert: Inserting a string char by char starting from the root node. Instantiating any internal TrieNode if necessary.
search: Starting from the root, check character by character. If the TrieNode that corresponds to the char is null, then we can infer that the prefix or string was not inserted before.

public class Trie {

    private TrieNode root;

    public Trie() {
        root = new TrieNode();
    }
    
    public void insert(String word) {
        TrieNode curr = root;
        int index;
        char[] charArr = word.toCharArray();
        for (char c : charArr) {
            index = c - 'a';
            if (curr.children[index] == null) {
                curr.children[index] = new TrieNode();
            }
            curr = curr.children[index];
        }
        curr.isEnd = true;
    }
    
    public boolean search(String word) {
        TrieNode curr = root;
        int index;
        char[] charArr = s.toCharArray();
        for (char c : charArr) {
            index = c - 'a';
            if (curr.children[index] == null) {
                return null;
            }
            curr = curr.children[index];
        }

        return curr;
    }

    public static class TrieNode {
        TrieNode[] children;
        boolean isEnd;

        public TrieNode() {
            this.children = new TrieNode[26];
            isEnd = false;
        }
    }
}

In most cases, we need only to deal with lower-case English letters, so we can use an array to store child nodes. One can also use a dictionary (A map) to implement the data structure, but under most cases using array is much faster.

LeetCode Problems #

If you want to practice implementing the data structure itself, you can start from those problems that directly require implementing the Trie.

421. Maximum XOR of Two Numbers in an Array #

Problem description #

Given an integer array nums, return the maximum result of nums[i] XOR nums[j], where 0 <= i <= j < n.

Example 1:

Input: nums = [3,10,5,25,2,8] Output: 28 Explanation: The maximum result is 5 XOR 25 = 28.

Example 2:

Input: nums = [14,70,53,83,49,91,36,80,92,51,66,70] Output: 127

Constraints:

1 <= nums.length <= 2 * 105
0 <= nums[i] <= 231 - 1

Naive solution #

A naive solution is to do a $O(n^2)$ XOR for every pair of numbers. Correct solution, but scales poorly for large input. Can we process every input number just once, resulting in $O(n)$ time complexity?

Using a binary trie to speed up #

Of course yes. The key insight is that to maximize the XOR of two numbers, we want their binary representations to differ in as many bit positions as possible, especially in the higher-order bits. XOR produces 1 when bits are different and 0 when they’re the same, so maximizing differences maximizes the result.

By storing all numbers in a binary Trie, we can efficiently find the number that produces maximum XOR with any given number by greedily choosing the opposite bit at each level, starting from the most significant bit.

Here is the code:

class Solution {
    public int findMaximumXOR(int[] nums) {
        if (nums.length < 2) {
            return 0;
        }

        int maxRes = 0;
        // insert the first number
        insert(nums[0]);

        for (int i = 1; i < nums.length; ++i) {
            maxRes = Math.max(maxRes, findMaxXOR(nums[i]));
            insert(nums[i]);
        }

        return maxRes;
    }

    private void insert(int num) {
        TrieNode curr = root;
        int bit;
        for (int i = 30; i >= 0; --i) {
            bit = (num >> i) & 1;
            if (curr.children[bit] == null) {
                curr.children[bit] = new TrieNode();
            }
            curr = curr.children[bit];
        }
    }

    private int findMaxXOR(int num) {
        int max = 0, bit, toggledBit;
        TrieNode curr = root;

        for (int i = 30; i >= 0; --i) {
            bit = (num >> i) & 1;
            toggledBit = 1 - bit;
            if (curr.children[toggledBit] != null) {
                max |= (1 << i);
                curr = curr.children[toggledBit];
            } else {
                curr = curr.children[bit];
            }
        }

        return max;
    }

    private static class TrieNode {
        TrieNode[] children;

        public TrieNode() {
            this.children = new TrieNode[2];
        }
    }

    private TrieNode root = new TrieNode();
}

To insert a number into the binary trie, we start from the most significant bit, and insert one bit into the binary trie at a time. Recall that for a signed integer, the leftmost bit is used for the sign, so we start from the second leftmost bit:

private void insert(int num) {
    TrieNode curr = root;
    int bit;
    
    // start from the second most significant bit
    for (int i = 30; i >= 0; --i) {
        bit = (num >> i) & 1;
	    // instantiate a new TrieNode if not present
        if (curr.children[bit] == null) {
            curr.children[bit] = new TrieNode();
        }
        // update curr
        curr = curr.children[bit];
    }
}

Starting from the second number, we search for the maximal possible XOR by searching the binary trie bit-by-bit like follows:

private int findMaxXOR(int num) {
    int max = 0, bit, toggledBit;
    TrieNode curr = root;

    for (int i = 30; i >= 0; --i) {
	    // to produce the maximal XOR, we search for the "complementary" bit
	    // that is, if the current bit is 1, we search for 0, and vice versa
        bit = (num >> i) & 1;
        toggledBit = 1 - bit;
        
        if (curr.children[toggledBit] != null) {
	        // if the toggledBit is present, then the bit at position i for the maximum should be 1
            max |= (1 << i);
            curr = curr.children[toggledBit];
        } else {
	        // if not, there is nothing to do except update the curr pointer
            curr = curr.children[bit];
        }
    }

    return max;
}

Complexity analysis #

Time Complexity: $O(n × 32) = O(n)$, where n is array length and 32 is the number of bits in an integer.
Space Complexity: $O(n × 32) = O(n)$ for the trie structure.

212. Word Search II #

Problem description #

Given an m x n board of characters and a list of strings words, return all words on the board.

Each word must be constructed from letters of sequentially adjacent cells, where adjacent cells are horizontally or vertically neighboring. The same letter cell may not be used more than once in a word.

Constraints:

m == board.length
n == board[i].length
1 <= m, n <= 12
board[i][j] is a lowercase English letter.
1 <= words.length <= 3 * 104
1 <= words[i].length <= 10
words[i] consists of lowercase English letters.
All the strings of words are unique.

!(e.g. 1)[2.png]

!(e.g. 2)[3.png]

Naive solution #

A naive solution is to do a DFS, searching for every single word in words. Resulting in $O(M \cdot N \cdot W \cdot 4^{L})$ time complexity, where:

M and N are the size of the matrix
W is the length of the input words
4^L is for one pass of DFS, where we search 4 directions for at most L steps. (L is the avg length of words)

The naive solution is no doubt correct, but it fails for large input size as you can imagine:

!(A TLE test case)[4.png]

Let’s first reason why our naive solution failed.

Redundant Searches: If many words share the same prefix, the common prefix is searched for each word with a full pass of DFS -> duplicate searches.
No Early Termination: We continue DFS even when the current path cannot lead to any word in the dictionary.
- e.g., if the common prefix aaaaaaa (from the TLE test case shown above) does not exist in the matrix at all, we still perform a full DFS.
  - !(A long common prefix exist for every keyword)[5.png]
- We should stop searching once we can tell the keyword doesn’t exist at all.
Inefficient Prefix Checking: For each cell and each word, we start from scratch without utilizing information from previous DFS. We do plain DFS over and over again.

All the shortcomings mentioned above lead to poor scalability for the naive DFS approach.

Speed up by storing keywords in a trie #

Remember, the trie data structure is efficient for doing prefix matching. Besides, it can prune a lot of search space once the current char is not present in the trie, leading to early termination.

We can first insert all the keywords into a trie, after then we do a single round of DFS to search all possible word combinations. During the search, if the char in the current DFS call is not present in the trie, we are sure that there is no meaning to go further, so we backtrack.

This is how it works:

class Solution {

    public List<String> findWords(char[][] board, String[] words) {
        m = board.length;
        n = board[0].length;

        // insert words into the trie
        buildTrie(words);

        for (int i = 0; i < m; ++i) {
            for (int j = 0; j < n; ++j) {
                dfs(board, i, j, root);
            }
        }

        return res;
    }

    private void dfs(char[][] board, int x, int y, TrieNode curr) {
        char c = board[x][y];
        int idx = c - 'a';
        if (curr.children[idx] == null) {
            return;
        }

        curr = curr.children[idx]; // update current TrieNode
        board[x][y] = '#'; // set a flag

        // match a word
        if (null != curr.key) {
            res.add(curr.key);
            curr.key = null;
            // shouldn't return here
        }

        for (int[] dir : dirs) {
            int newX = x + dir[0], newY = y + dir[1];
            if (newX < 0 || newX >= m || newY < 0 || newY >= n || '#' == board[newX][newY]) {
                continue;
            }
            dfs(board, newX, newY, curr);
        }

        // backtrack
        board[x][y] = c;
        return;
    }

    private class TrieNode {
        TrieNode[] children;
        String key;

        public TrieNode() {
            children = new TrieNode[26];
        }
    }

    private void buildTrie(String[] words) {
        root = new TrieNode();
        for (String w : words) {
            insert(w);
        }
    }

    private void insert(String word) {
        TrieNode curr = root;
        int idx;
        for (char c : word.toCharArray()) {
            idx = c - 'a';
            if (curr.children[idx] == null) {
                curr.children[idx] = new TrieNode();
            }
            curr = curr.children[idx];
        }
        curr.key = word;
    }

    private int[][] dirs = new int[][] {{-1, 0}, {1, 0}, {0, -1}, {0, 1}};
    private int m;
    private int n;
    private TrieNode root;
    List<String> res = new LinkedList<>();
    
}

We first build the trie by inserting each String in words:

private void buildTrie(String[] words) {
    root = new TrieNode();
    for (String w : words) {
        insert(w);
    }
}

private void insert(String word) {
    TrieNode curr = root;
    int idx;
    for (char c : word.toCharArray()) {
        idx = c - 'a';
        if (curr.children[idx] == null) {
            curr.children[idx] = new TrieNode();
        }
        curr = curr.children[idx];
    }
    curr.key = word;
}

Note that we store the keyword into the TrieNode if it represents the end of a keyword, so we don’t need to bother manipulating chars along the DFS and backtracking:

private class TrieNode {
    TrieNode[] children;
    String key;  // directly stores key into the TrieNode

    public TrieNode() {
        children = new TrieNode[26];
    }
}

Then, we do a DFS once for all:

private void dfs(char[][] board, int x, int y, TrieNode curr) {
    char c = board[x][y];
    int idx = c - 'a';
    if (curr.children[idx] == null) {
        return;
    }

    curr = curr.children[idx]; // update current TrieNode
    board[x][y] = '#'; // set a flag

    // match a word
    if (null != curr.key) {
        res.add(curr.key);
        curr.key = null;
        // shouldn't return here
    }

    for (int[] dir : dirs) {
        int newX = x + dir[0], newY = y + dir[1];
        if (newX < 0 || newX >= m || newY < 0 || newY >= n || '#' == board[newX][newY]) {
            continue;
        }
        dfs(board, newX, newY, curr);
    }

    // backtrack
    board[x][y] = c;
    return;
}

Two details to clarify:

Since we directly store keywords into TrieNode, if there is a match, we add the key into res and delete it to avoid duplicate keyword in the final res:

// match a word
if (null != curr.key) {
    res.add(curr.key);
    curr.key = null;
    // shouldn't return here
}

We use the matrix itself to denote whether or not we have visited a cell before—by setting the cell to a special char (in our example, a #) and resetting it back when we backtrack. This is a very common technique to use for DFS/backtracking problems.

private void dfs(char[][] board, int x, int y, TrieNode curr) {
    // recording the original char
    char c = board[x][y];
    
    // ...

	// setting the char into `#`
    board[x][y] = '#';

    // ...

    // resetting the char
    board[x][y] = c;
    return;
}

Complexity analysis #

$O(M \cdot N \cdot W \cdot 4^{L})$

Time complexity: $O(W \cdot L + M \cdot N \cdot 4^{L})$, where
- $O(W \cdot L)$ is used for building the trie, W is the length of words, and L is the avg word length
- $O(M \cdot N \cdot 4^L)$ is for the DFS part. This time we only perform one pass of DFS with pruning, leading to roughly $W \cdot M \cdot N \cdot 4^L$ times speed up.
Space complexity: $O(W \cdot L)$ for storing the keywords in the trie.