Lowest Common Ancestor #

From Wikipedia Lowest common ancestor - Wikipedia page:

In graph theory and computer science, the lowest common ancestor (LCA) (also called least common ancestor) of two nodes v and w in a [tree]( https://en.wikipedia.org/wiki/Tree_ (graph_theory) “Tree (graph theory)") or directed acyclic graph (DAG) T is the lowest (i.e. deepest) node that has both v and w as descendants, where we define each node to be a descendant of itself (so if v has a direct connection from w, w is the lowest common ancestor).

The definition is simple. Let’s see some examples:

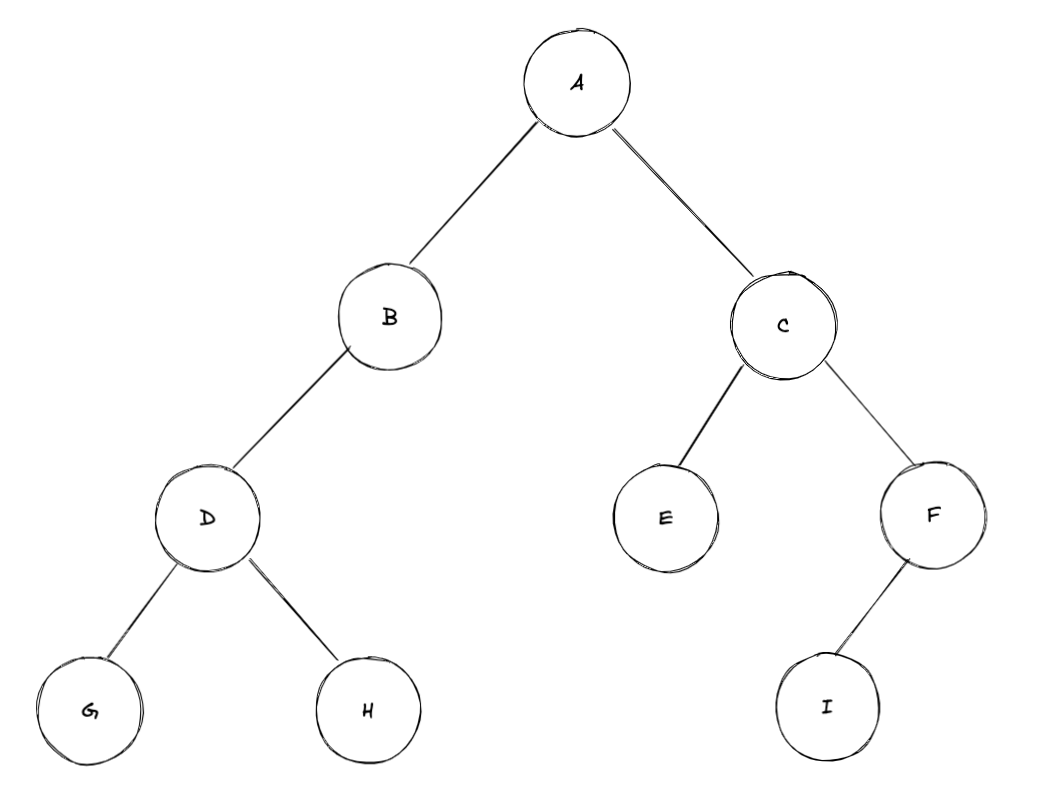
• The LCA of A and B is A;
• The LCA of B and C is A;
• The LCA of D and E is A;
• The LCA of E and I is C;
• The LCA of D and F is A;
• The LCA of G and H is D;
• The LCA of C and F is C;

How to find the LCA of two nodes in a tree? #

Almost all binary tree problems use a recursive algorithm, this is due to the local structure property of the tree data structure: each node only stores its local information, we cannot access global tree data from any single node.

So, at each node, we process the “current” data and node locally, and return it to its parent via the recursive calls: when the recursive function call returns to the parent, local information is passed and kept. Thus we can construct the final and global results by recursively processing and passing information.

The idea to get the LCA of any two nodes, say A and B, also applies the recursive method:

• Starting from the bottom up, if the current node is either A or B, return the node itself to its parent where the recursion starts. If the current node is neither one, return a null.
• When two recursive calls return from the left and right child, the parent can determine whether it is the LCA by checking whether the returns are null or not:
  • If both returns are not null, the parent node can infer that it is actually the LCA of A and B
  • If one is null and the other is not, the parent can tell that the non-null node returned is either the LCA or one of the target nodes, it can safely return the non- null node
  • If both are null, the parent know that the subtree starting at it does not hold A and B, it can simply returns null

For any given node A and B, their LCA is:

• Case 1: A parent node exists above.
• Case 2: A or B itself, which means one of the target is the ancestor of the other one.

Which means during our recursive call, both of the returns are not null can happen at most one time (for case 1). In such a case, the current node must be the LCA.

For case 2, the base case check in the recursive algorithm can safely return the LCA:

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null) {
            return null;
        }
        
        if (root == p || root == q) {
            return root;
        }
        
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        
        if (left != null && right != null) {
            return root;
        } else if (left != null) {
            return left;
        } else {
            return right;
        }
    }
}

Sample problems #

1123. Lowest Common Ancestor of Deepest Leaves #

Given the root of a binary tree, return the lowest common ancestor of its deepest leaves.

Recall that:

• The node of a binary tree is a leaf if and only if it has no children
• The depth of the root of the tree is 0. if the depth of a node is d, the depth of each of its children is d + 1.
• The lowest common ancestor of a set S of nodes, is the node A with the largest depth such that every node in S is in the subtree with root A.

Example 1:

![[2.png]]

Input: root = [3,5,1,6,2,0,8,null,null,7,4] Output: [2,7,4] Explanation: We return the node with value 2, colored in yellow in the diagram. The nodes coloured in blue are the deepest leaf-nodes of the tree. Note that nodes 6, 0, and 8 are also leaf nodes, but the depth of them is 2, but the depth of nodes 7 and 4 is 3.

Example 2:

Input: root = [1] Output: [1] Explanation: The root is the deepest node in the tree, and it’s the lca of itself.

Example 3:

Input: root = [0,1,3,null,2] Output: [2] Explanation: The deepest leaf node in the tree is 2, the lca of one node is itself.

Solution #

To solve the problem, we need two separate steps:

1. Find the deepest leaves;
2. Return their LCA

Multiple (more than 2) deepest leaves can exist at the same time, our algorithm still holds because:

1. For the deepest node, it returns itself.
2. For any internal node, it still checks the returns from its children:
   1. If both the returns are null -> the subtree starting at it does not hold any deepest node;
   2. If any of the return is not null -> the return is LCA
   3. If both of the return is not null -> the current internal node is the LCA

class Solution {
    private int deepestDepth = 0;

    public TreeNode lcaDeepestLeaves(TreeNode root) {
        if (root.left == null && root.right == null) {
            return root;
        }
        findDeepestDepth(root, 0);
        return lca(root, 0);
    }

    private TreeNode lca(TreeNode root, int depth) {
        if (root == null) {
            return null;
        }

        TreeNode leftRet = lca(root.left, depth + 1);
        TreeNode rightRet = lca(root.right, depth + 1);

        if (depth == deepestDepth) {
            return root;
        }

        if (leftRet != null && rightRet != null) {
            return root;
        } else if (leftRet != null) {
            return leftRet;
        } else {
            return rightRet;
        }
    }

    private void findDeepestDepth(TreeNode root, int depth) {
        if (root == null) {
            return;
        }
        deepestDepth = Math.max(deepestDepth, depth);
        findDeepestDepth(root.left, depth + 1);
        findDeepestDepth(root.right, depth + 1);
    }
}

235. Lowest Common Ancestor of a Binary Search Tree #

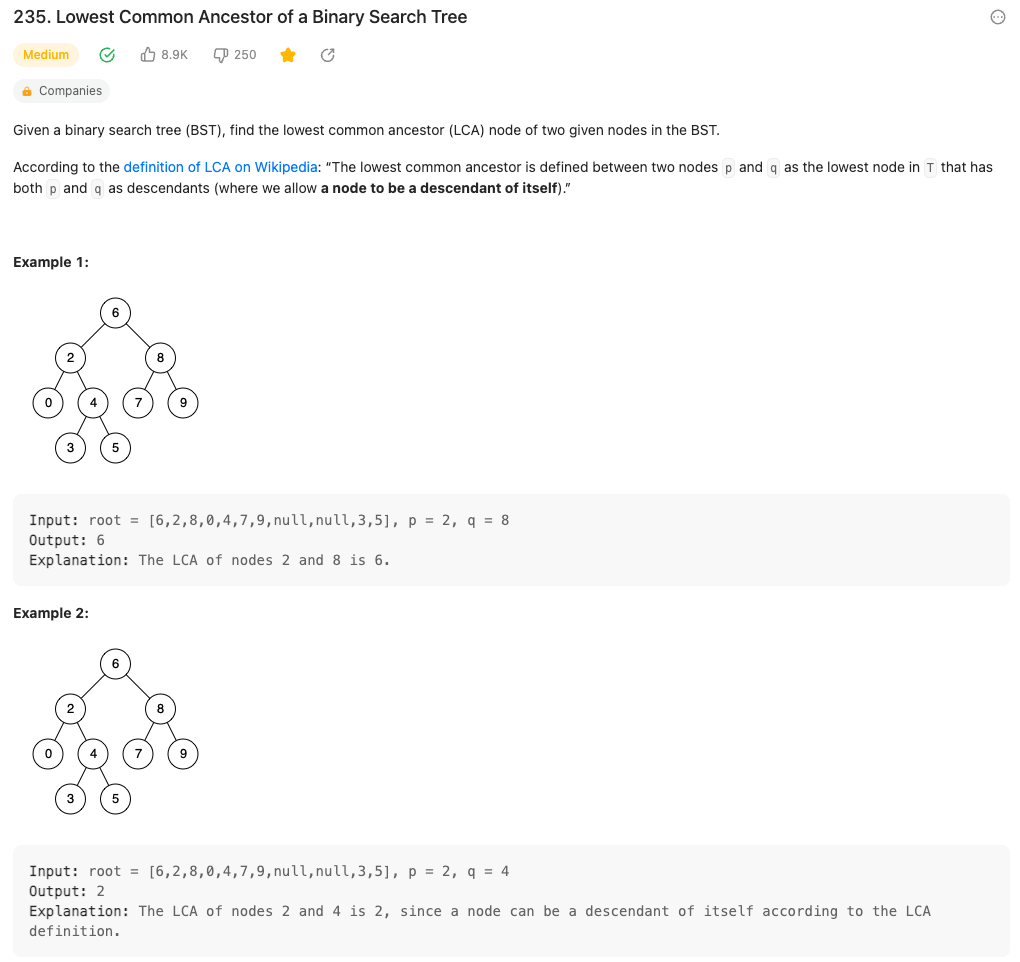
The difference is that we switch to binary search tree. It has the following property:

For any given node A and B, their LCA must obeys A.val <= LCA.val && LCA.val <= B.val if A.val <= B.val.

So, during recursive calls, we do not check the nullity of returns anymore. For this problem, we check whether the internal node satisfies the boolean statement mentioned above:

• If curr.val < A.val && curr.val < B.val, then the current node’s value is too small, we need to find the LCA from its right subtree;
• If curr.val > A.val && curr.val > B.val, then the curr.val is too large, we search the LCA from its left subtree
• If curr.val > A.val && curr.val < B.val, the curr node must be the LCA

Then algorithm works as follows:

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root.val > p.val && root.val > q.val) {
            return lowestCommonAncestor(root.left, p, q);
        } else if (root.val < p.val && root.val < q.val) {
            return lowestCommonAncestor(root.right, p, q);
        } else {
            return root;
        }
    }
}

Other LCA problems #

1. 235. Lowest Common Ancestor of a Binary Search Tree
2. 236. Lowest Common Ancestor of a Binary Tree
3. 865. Smallest Subtree with all the Deepest Nodes
4. 1123. Lowest Common Ancestor of Deepest Leaves