Construct Binary Tree From inorder/preorder/postorder Traversal
This post analyzes how to construct a bst from its preorder/postorder/inorder traversals
· 8 min read
Can we construct a BST from any 2 of its preorder/postorder/inorder traversals (actually, traversal sequences)? The answer is yes. In order to understand why we can do so, we need to have a deep understanding of the properties not only of BST but also of its traversals.
We briefly recap the BST data structure first:
class TreeNode {
int val;
TreeNode left;
TreeNode right;
TreeNode() {
}
TreeNode(int val) {
this.val = val;
}
TreeNode(int val, TreeNode left, TreeNode right) {
this.val = val;
this.left = left;
this.right = right;
}
public static void preorder(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
list.add(root.val);
preorder(root.left, list);
preorder(root.right, list);
}
public static void postorder(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
postorder(root.left, list);
postorder(root.right, list);
list.add(root.val);
}
public static void inorder(TreeNode root, List<Integer> list) {
if (root == null) {
return;
}
inorder(root.left, list);
list.add(root.val);
inorder(root.right, list);
}
}
inorder | preorder | postorder | |
|---|---|---|---|
| Node Traversal Order | root.left -> root -> root.right | root -> root. left -> root.right | root.left -> root.right -> root |
| The position of subroot within subsequence (where subsequence refers to the sequence obtained by traversing the subtree rooted at subroot) | Can not be determined solely by inorder | subseq[0] | subseq[sublist.length - 1] |
| Properties | According to the nature of preorder traversal, the next element in the current subtree sequence after the subroot must be subroot.left (if it exists).That is: subroot.left = subseq[1] | According to the nature of postorder traversal, the element right before the subroot in the current subtree sequence must be subroot.right (if it exists).That is: subroot.right = subseq[subseq.length - 2] | |
| Subsequence Structure | [left subtree sequence] [subroot] [right subtree sequence] | [subroot] [left subtree sequence] [right subtree sequence] | [left subtree sequence] [right subtree sequence] [subroot] |
We can easily get the subroot from preorder and postorder traversal subsequences, since the subroot must be positioned at the first and the last index, which can be inferred from the properties of preorder and postorder recursive calls.
But we cannot infer the position of the subroot solely from the inorder sequence: the position of the subroot seems to be arbitrary. But, if we can tell the position of the subroot from preorder or postorder sequences, we can determine the range of subroot.left and subroot.right by:
- Find the position of the
subrootin theinordersequence - According to the property of
inordertraversal, all elements that appear before thesubrootare its left children, all elements that follow thesubrootare its right children
As mentioned in my previous blog LeetCode Lowest Common Ancestor Problems | Lihang Liu’s Homepage, almost all binary tree problems are solved in recursion. If we are given inorder traversal sequence of a BST + one of its postorder or preorder traversal sequence, we can rebuild the BST by recursively finding the subroot and partitioning its left children and right children.
Let’s see the problems.
105. Construct Binary Tree from Preorder and Inorder Traversal #

Let’s first clarify the variables we’re going to use:
rootPreIndex: The index of thesubrootin thepreordersequencerootInorderIndex: The index of thesubrootin theinordersequenceinorderLeftandinorderRight: refer to the recursion range for the subtree, i.e.,inorder[inorderLeft : inorderRight]is theinordersequence of the subtree. It is also used to control our recursive functions- The length (size) of the left subtree:
leftSubtreeSize = rootInorderIndex - inorderLeft
The algorithm works as follows:
- We recursively built the BST using this
TreeNode build(int[] preorder, int[] inorder, int rootPreIndex, int inorderLeft, int inorderRight)function - Find the
subrootfrom thepreordersubarr, thesubrootis always the first element inpreordersubarr, call the constructor to instantiate thesubrootnode - Determines the index of
subroot, i.e.rootInorderIndex, ininordersubarr - Recursively built the left subtree:
- The index of
subroot.leftin thepreorderisrootPreIndex + 1 - The
inorderLeftfor the left subtree is the currentinorderLeft - The
inorderRightfor the right subtree isrootInorderIndex - 1 - Call
build(preorder, inorder, rootPreIndex + 1, inorderLeft, rootInorderIndex - 1)
- The index of
- Recursively built the right subtree:
- The index of
subroot.rightin thepreorderisrootInorderIndex + leftSubtreeSize + 1 - The
inorderLeftfor the right subtree isrootInorderIndex + 1 - The
inorderRightfor the right subtree isinorderRight - Recursively build right subtree by calling
build(preorder, inorder, rootPreIndex + leftSubTreeSize + 1, rootInorderIndex + 1, inorderRight)
- The index of
class Solution {
public TreeNode buildTree(int[] preorder, int[] inorder) {
return build(preorder, inorder, 0, 0, inorder.length - 1);
}
public TreeNode build(int[] preorder, int[] inorder, int rootPreIndex, int inorderLeft, int inorderRight) {
if (inorderLeft > inorderRight || rootPreIndex < 0 || rootPreIndex >= preorder.length) {
return null;
}
TreeNode root = new TreeNode(preorder[rootPreIndex]);
int rootInorderIndex = -1;
for (int i = 0; i < inorder.length; ++i) {
if (inorder[i] == root.val) {
rootInorderIndex = i;
break;
}
}
int leftSubTreeSize = rootInorderIndex - inorderLeft;
root.left = build(preorder, inorder, rootPreIndex + 1, inorderLeft, rootInorderIndex - 1);
root.right = build(preorder, inorder, rootPreIndex + leftSubTreeSize + 1, rootInorderIndex + 1, inorderRight);
return root;
}
}
106. Construct Binary Tree from Inorder and Postorder Traversal #
This problem does not differ a lot from 105. Construct Binary Tree from Preorder and Inorder Traversal we have covered. So I just leave my solution here:
class Solution {
public TreeNode buildTree(int[] inorder, int[] postorder) {
return build(inorder, postorder, postorder.length - 1, 0, inorder.length - 1);
}
public TreeNode build(int[] inorder, int[] postorder, int rootPostIndex, int inorderLeft, int inorderRight) {
if (inorderLeft > inorderRight || rootPostIndex < 0 || rootPostIndex >= postorder.length) {
return null;
}
TreeNode root = new TreeNode(postorder[rootPostIndex]);
int rootInorderIndex = -1;
for (int i = 0; i < inorder.length; ++i) {
if (inorder[i] == root.val) {
rootInorderIndex = i;
break;
}
}
int rightSubTreeLen = inorderRight - rootInorderIndex;
root.left = build(inorder, postorder, rootPostIndex - rightSubTreeLen - 1, inorderLeft, rootInorderIndex - 1);
root.right = build(inorder, postorder, rootPostIndex - 1, rootInorderIndex + 1, inorderRight);
return root;
}
}
889. Construct Binary Tree from Preorder and Postorder Traversal #
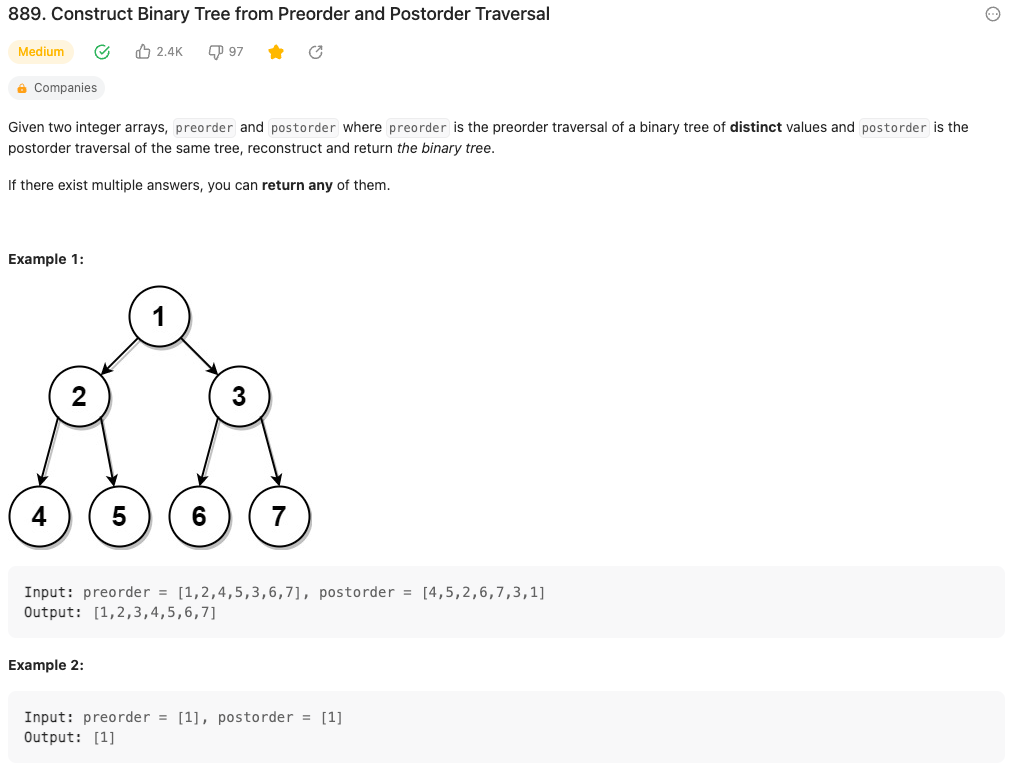
This problem is a little bit different from the previous two, we no longer have an inorder sequence to determine the left and right subtrees.
But, from the properties of postorder and preorder, we can still infer the ranges for both subroot.left and subroot.right subtress in the preorder and postorder. Take the example shown in the problem:
- The
rootis 1, it is the first element inpreorderand the last element inpostorder root.leftis 2, which is right afterrootinpreorder, and right beforerootinpostorder- From here, we can do a linear scan to find the index of
root.leftin thepostordersubsequence. Note that the index forroot.leftin the left subtree is denoted asleftSubRootPostIndex - After obtaining the position of
root.leftinpostorder, we can calculate the length of the left subtree using:leftSubtreeLength = leftSubRootPostIndex - postLeft + 1 - In the example,
root.leftis 2, and its index inpostorderis2, so the length of the left subtree is2 - 0 + 1 = 3
- From here, we can do a linear scan to find the index of
- After obtaining the length of the left subtree, we can calculate the range of the left and right subtree in
preorderandpostorder: - For the left subtree:
- The
preorderstarts atrootPreIndex + 1, ends atrootPreIndex + leftSubtreeLength(ps, in the code,rootPreIndexis namedpreLeft) - The
postorderstarts atpostLeft, ends atpostLeft + leftSubtreeLength - 1, this can be inferred from the properties of post-order traversal
- The
- For the right subtree:
- The
preorderstarts atpreLeft + leftSubtreeLength + 1, ends atpreRight - The
postorderstarts atpostLeft + leftSubtreeLengthends atpostRight - 1
- The
As you can see, we can infer the ranges for the subtrees by combining the information obtained from both traversals:
- From the
preorder, we knowrootispreorder[0],root.leftispreorder[1] - Once we know
root.left, we can do a linear scan to find its index inpostorder - Once we know the index of
root.leftinpostorder, we can calculate the length of the left subtree - Once we know the length of the left subtree, the length of the right subtree, plus the starting and ending index for
preorderandpostorderfor the recursive calls, can be calculated
Can we build the solution using the length of the right subtree? Of course we can. Since root.right appears right before the root in postorder, we can do a linear scan to find its index in preorder, then we can calculate the length of the right subtree. The implementation is different, but the idea is similar.
class Solution {
public TreeNode constructFromPrePost(int[] preorder, int[] postorder) {
return build(preorder, postorder, 0, preorder.length - 1, 0, postorder.length - 1);
}
private TreeNode build(int[] pre, int[] post, int preLeft, int preRight, int postLeft, int postRight) {
if (preLeft > preRight) {
return null;
}
TreeNode root = new TreeNode(pre[preLeft]);
if (preLeft + 1 > preRight) {
return root;
}
int leftSubRootPostIndex;
for (leftSubRootPostIndex = postLeft; leftSubRootPostIndex <= postRight; ++leftSubRootPostIndex) {
if (post[leftSubRootPostIndex] == pre[preLeft + 1]) {
break;
}
}
int leftSubtreeLength = leftSubRootPostIndex - postLeft + 1;
root.left = build(pre, post, preLeft + 1, preLeft + leftSubtreeLength, postLeft, postLeft + leftSubtreeLength - 1);
root.right = build(pre, post, preLeft + leftSubtreeLength + 1, preRight, postLeft + leftSubtreeLength, postRight - 1);
return root;
}
}
Recap #
Given two sequences from inorder/preorder/postorder traversals of a binary tree, we can rebuild the binary tree by combining information from both traversals.
We can first determine the index of the root in both traversals. From there, given the properties of inorder/preorder/postorder traversals, we can easily tell the index for root.left or root.right. Then we can determine the length or the range for the left and right subtrees. Once we inferred the ranges, we can rebuild the original binary tree using recursive function calls.